| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- CommunicateWiththeWorld
- 스몰토크
- 성내동장어
- #nlp
- #영어발음교정
- 화상영어
- #링글
- #영어공부
- #Ringle
- 강동구장어맛집
- 둔촌역장어
- #체험수업
- 영어로전세계와소통하기
- 장어랑고기같이
- 링글커리어
- 영어공부법
- 소통챌린지
- 영어회화
- 해외취업컨퍼런스
- 링글리뷰
- 영어시험
- 뉴노멀챌린지
- 링글경험담
- Ringle
- #직장인영어
- #링글후기
- 총각네장어
- 링글
- 영어공부
- 오피스밋업
- Today
- Total
Soohyun’s Machine-learning
[PRML] 2.1~2.2.1 Probability Distributions 본문

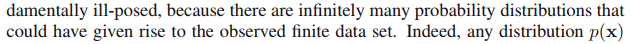
주어진 finite set x1, ... , xN (데이터)에서, random variable x의 probability distribution p(x)를 모델링하는 것을 density estimation이라고 한다.
이 챕터에서 나오는 모든 분포들은 Bayesian 관점에서의 prior들이며, i.i.d 하다고 가정한다. 그리고 이 분포들은 exponential family에 속한다.
i.i.d : independent and identically distributed
| Random variables 란? - 확률 현상에 기인해서 결과값이 확률적으로 정해지는 변수 constant : 상수, 정해져 있는 값 variable : 변수, 확률적으로 변할 수 있는 수 |
아래는 이 챕터에서 다루는 parametric distributions의 세부적인 예시들이다.
- Discrete random variables : binomial & multinomial distribution
- Continuouts random variables : Gaussian distribution
frequentist 관점에선, 파라미터들을 특정한 값으로 선택한다. e.g.) likelihood function
bayesian 관점에선, 파라미터들에 대한
1) prior distribution이 있고
2) 주어진 데이터에 대해서 대응하는 posterior distribution을 Bayes Theorem으로 계산한다.
또한 이 챕터의 분포들에는 conjugacy가 있는데, conjugacy란..
e.g.) Gaussian (prior) x likelihood function = Gaussian (posterior)
즉, prior의 분포와 posterior의 분포가 동일한 것을 나타낸다.
이런 parametric 접근법의 한계점은, 분포에 대한 특정한 functional form을 가정한다는데에 있다. 즉, prior로 Gaussian을 가정했는데, 데이터가 이 분포로 approximation이 잘 안되는 형태라면 ... prior로서의 Gaussian 가정 자체가 독이 된다.
본 챕터 뒤에서 non-parametric approach인 histograms / nearest-neighbors / kernels 를 소개한다.
| 2.1. Binary Variables |
single binary random variables x ∈ {0,1}
x : outcome of flipping coin (코인 플립을 한 결과)
1 : head
0 : tail
이게 fair coin이면 1과 0이 나올 확률이 0.5로 동일할텐데, 부서진 코인이라서 확률이 다르다고 가정한다.
그럼 x = 1일때의 확률을 μ로 표현하면, 아래와 같다.

이는 x라는 event가 1에 대해서 True일 때를 말한다.
probability이므로 0 <= μ <= 1 이다. 그러므로 x = 0의 확률은 아래와 같다.
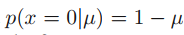
x 전반에 대한 probability distribution은 아래와 같이 쓸 수 있으며, Bernoulli distribution (베르누이 분포)이라고 한다.

이 distribution의 mean은 아래와 같고
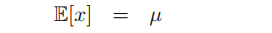
이 distribution의 variance는 아래와 같다.

이제 데이터셋 D = {x1, ... , xN}이 변수 x에 대해서 관측된 값들이고, μ에 대한 함수 p(x|μ)로부터 i.i.d하게 그려진다고 가정하고 likelihood function을 만들어보자.
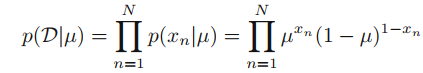
수식만 보면 왜 μ를 maximize해야 하는지 직관적으로 이해가 가지 않는데, 데이터셋인 D는 이미 고정된 상태이므로, 이 D를 만들어내는 μ를 찾는 것 (maximize)이기 때문이다. 즉, likelihood function을 maximize함으로써 μ를 estimate하는 것이다.
그런데 사실 값의 절대적인 수치가 아닌 max가 의미가 있는 것이면, 여기에다가 log를 붙여서 computational cost를 줄일 수 있다.
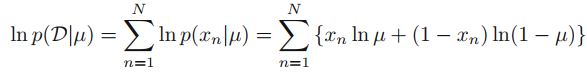
복잡해보이지만 i.i.d 가정이므로 P(X,Y) = P(X)P(Y)임을 기억하면 이해하기가 쉽다. 곱하기가 log가 붙어서 더하기가 된 것.
위의 수식에서 μ를 편미분해 서 0이 되는게 max이므로 아래의 공식이 나온다.

위를 sample mean이라고도 한다. 앞의 1/N은 그냥 normalization factor이다.
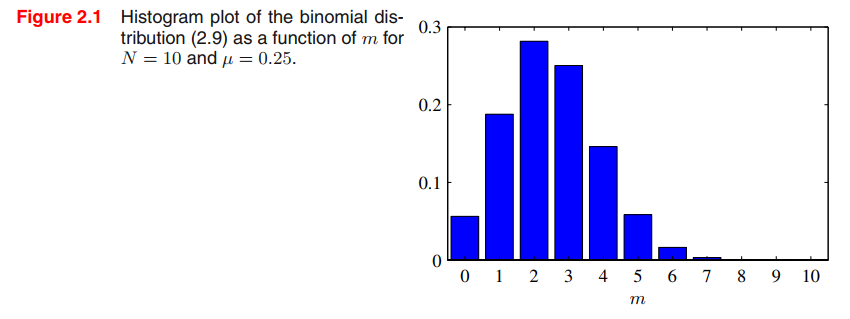
여기서 m은 x=1 (헤드)이 나온 빈도수를 말하며, 0은 x=1이 한 번도 안 나온 경우를 말한다.
N은 총 시행 횟수를 말한다.

만약 3번의 trials이 있었고, 헤드(x=1)가 3번이 나왔다면 N=m=3이고 μML=1이다.
이런 말도 안되는 상황을 피하기 위해서, prior distribution을 넣어준다.

여기서는 m만 변화가 가능하다. (N인 trials 횟수는 고정이고, μ는 m/N에 의해서 결정되는 것이므로)
앞의 combination은 아래와 같은 수식으로 정의된다.
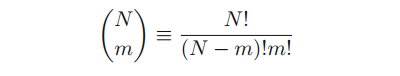
N개의 같은 오브젝트들에 대해서 m개의 오브젝트를 선택하는 방법. 이게 comb 맞나?
Binomial distribution의 mean & variance는


아래의 variance는 직관적으로 보면 Bin(m|N,μ)가 확률 변수의 분포니까
(m-E[m])^2로 그냥 scailing을 해준거라고 보면 이해가 될 것 같다. (맞나?)
베르누이는 결과가 True / False 두 가지인 경우를 뜻하며, 베르누이 분포는 성공률이 p인 실험에서 성공이면 x=1, 실패이면 x=0이라고 하면, random variables x의 probability distribution을 parameter (모수) p인 베르누이 분포라고 한다.

이항분포는 매회 성공률이 p인 베르누이 실험을 독립적으로 n번 반복할 때, 성공한 횟수(flipping coin 예시에서는 x=1, head인 경우)의 확률 분포를 parameter (모수) n과 p인 이항 분포라고 한다.
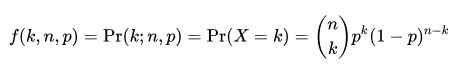
여기서 k는 x=1(헤드, 성공한 횟수)이고, 앞 부분 (n k)는 combination을 말한다.
http://blog.naver.com/PostView.nhn?blogId=qbxlvnf11&logNo=221353346955
| 2.1.1. The Beta Distribution |
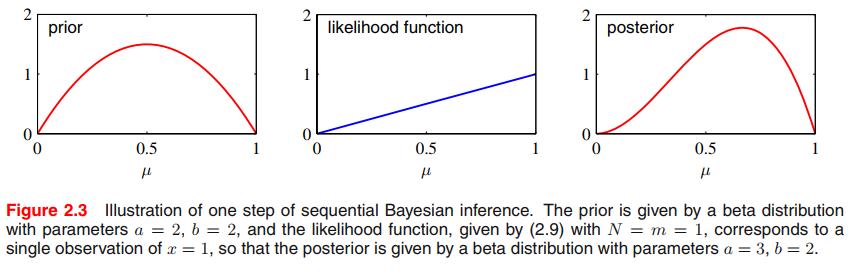
앞에서 보았듯이 frequentist 관점으로만 생각하면, 시행횟수 3번, 헤드 3번, μ=1이라는 참사가 날 수 있다. 이제 Bayesian 관점에서 보자. 모수 μ에 대한 prior distribution p(μ)를소개한다.
prior로 Beta distribution을 보자.

Γ(.)는 gamma function
좌측의 Beta()가 posterior이며, 중간의 Γ(.) 부분이 normalization coefficient이고, 뒤의 μ^(a-1) * (1-μ)^(b-1)이 likelihood function이다.
위의 수식에서의 normalization coef.는 베타 분포가 normalized 되어 있음을 확실하게 알 수 있다. 그러므로..
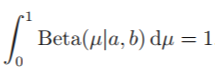
또한 베타 분포에서의 mean은 아래와 같이 정의되고

variance는 아래와 같이 정의된다.

여기서 a,b는 hyperparameters고, 이 a,b가 μ의 distribution을 만든다.

μ에 대한 posterior distribution은
beta prior (2.13)와

binomial likelihood function (2.9) 그리고 normalizing으로 얻을 수 있다.

μ에 대해서 의존하는 factors만 남겼을 때, posterior distribution은 아래와 같은 형태를 한다.

여기서 l (L) = N-m으로, 이전의 flipping coin 예시에서 tail 이라고 보면 된다.
앞의 Beta distribution 수식에 normalization coef.가 합쳐진 Beta의 모습은..

a는 m의 값에 의해, b는 l의 값에 의해 증가할 수도, 줄어들 수도 있다.
그리고 posterior distribution은 차후 추가되는 데이터들에 대해서 prior가 될 수도 있다. 수식으로 보면..
Beta(a', b') = Bin(m,l) Beta(a,b)
----------- -----------
posterior prior = 이전 beta의 posterior / 현재의 prior
|----------------------------|
prior의 dist와 posterior의 dist가 동일하다 = conjugate prior
이를 통해 달성하려는 목표가 "다음 trial의 outcome을 가장 잘 예측하는 것"이라면, 아래와 같이 수식을 쓸 수 있다.
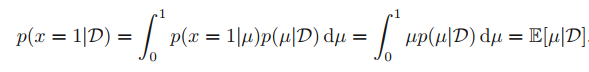
D : 데이터셋
앞에서 보았던 Beta의 mean인 E[μ]=a/a+b와 normalization coef.인 m, l을 넣으면 아래와 같은 수식이 나온다.
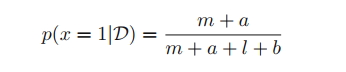
x의 predictive distribution을 evaluate 한 것이다.
데이터가 많아질수록 posterior distribution에 나타나는 uncertainty는 줄어든다. => θ에 대한 확실성이 올라간다.
이를 설명하기 위해서, Bayesian learning의 frequentist view를 채택한다.
파라미터 θ에 대한 Bayesian inference problem을 생각해보자. joint distribution p(θ,D)로 설명해보자면

위의 수식은 아래의 θ의 mean에 대한 정의가 성립하고 있을 때, 가능하다.

이는 θ에 대한 posterior mean (데이터를 생성해내는 distribution 전반에 걸친 평균)이 θ에 대한 prior mean과 같음을 알 수 있다. 같은 맥락으로 variance를 보면..

(θ에 대한 prior variance) = (θ에 대한 posterior variance의 평균) + (θ의 posterior mean의 variance를 측정하는 부분)
보통 θ의 posterior variance는 prior variance보다 적다. 하지만 특정 상황에서는 posterior variance가 prior variance보다 클 수도 있다는 것도 기억해두자.
| 2.2 Multinomial Variables |
1-of-K : 원 핫 인코딩을 생각하면 된다.

이 벡터들은 아래 조건을 만족한다.
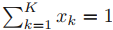
만약 파라미터
μ_(k)를 써서 x_(k)=1의 확률을 나타낸다면, x의 distribution은 아래와 같다.
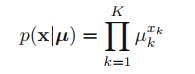
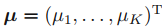
그리고 확률이기 때문에 (당연하게도) 각각의 mu_k는 0보다 크고, 전체 mu_k의 합은 1이 되는, 확률의 조건을 만족한다.
바로 위의 수식 (분포)은 베르누이 분포의 generalization (2개 이상의 outcomes를 낼 수 있는) 이라고 볼 수 있다. 분포가 정규화된 걸 쉽게 볼 수 있으므로 (??? 어떻게?) 아래의 수식을 만족하고
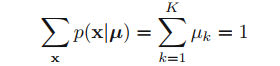
또 아래의 수식도 만족한다.
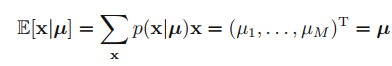
데이터셋 D를 N개의 독립적인 관측된 데이터들 x1, ..., xN 이라고 보면, 대응되는 likelihood function은 아래와 같은 형태를 띄게 된다.
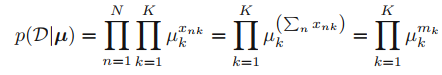

여기서 m_(k)를 sufficient statistics (충분 통계량)이라고 하며, 모수(parameters)를 추정할 수 있는 충분한 정보를 가진 값이라는 의미이다. (여기서는 모수가 μ)
(충분 통계량 출처 : https://datascienceschool.net/view-notebook/56e7a25aad2a4539b3c31eb3eb787a54/)
그리고 μ_(k)에 걸린 constraint (합이 1이 되어야 한다)를 만족하면서, μ를 위한 maximum likelihood solution을 찾기 위해서 Lagrange multiplier를 쓴다.
(라그랑주 승수법 : https://untitledtblog.tistory.com/96)
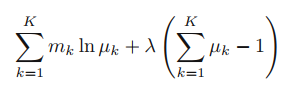
여기서 A+B를 maximize하나, A를 maximize하나 차이가 없다. 왜냐하면 μ_(k) constraint가 합쳐서 1이 된다는 것이므로, 뒤의 Term B는 항상 0이 되어야 하기 때문이다.
그리고 위의 수식을 μ_(k)로 미분해보면 m_(k)/μ_(k) + λ*1이 나오고, 이를 정리해서 아래와 같은 수식을 얻을 수 있다.

이 수식에 λ = -N을 적용해보면, 아래와 같은 maximum likelihood solution을 얻을 수 있다. (N : 총 시행 횟수)

이는 x_(k)=1인 observations N개에 대한 분수이다.
파라미터 μ에 의존하는, m1,...,m_(k)의 joint distribution을 생각해보자. p(D|μ)는 아래와 같으므로
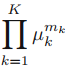
아래와 같은 형태가 나오는데
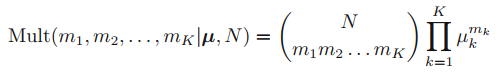
이를 multinomial distribution이라고 한다.

제약 조건에 의해서 m_(k)를 이렇게 구할 수 있는데, 결국 N이다.

| 2.2.1 The Dirichlet Distribution |
이제 위에서 소개한 multinomial distribution의 파라미터 {μ_(k)}를 위한 prior distribution의 family distribution을 소개한다.
multinomial distribution의 형태를 검증함으로써, conjugate prior는 아래와 같이 주어진다.

여기에서의 μ_(k) 역시 probability 조건이 걸려있다. (0보다 크며, 다 합치면 1이 됨)
위의 수식에서의 α1, ..., α_(K)는 분포의 파라미터들을 의미하며,
α = (α1,...,α_(K))^T
summation constraint 때문에 {μ_(k)} space에서의 distribution은 K-1 차원을 갖는 simplex이다.

이 분포의 normalized form은 아래와 같은 수식을 통해 나타낼 수 있으며, Dirichlet distribution이라고 한다.

Γ(.)는 gamma function이며 아래와 같은 수식으로 나타낸다.
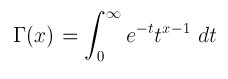

감마 함수의 시작은 오일러가 "기호 n! 같은 계승(階乘, factorial)은 왜 정수에만 정의되지? 이 함수를 실수로 확장하는 방법이 없을까?'로 인해 시작되었다고 한다.
(출처 : https://ghebook.blogspot.com/2011/12/gamma-function.html)
아래의 수식을 보면 특이한 점이 하나 있는데, α0가 normalization term, 그 중에서도 분자에만 존재한다는 점이다.

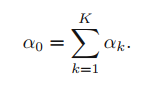
α0는 위와 같이 정의되기 때문에, α0는 표현형만 alpha를 썼을 뿐, 그냥 α1~α_(k)까지의 합을 나타내는 아이라고 볼 수 있다.
Dirichlet distribution의 prior는 아래와 같고
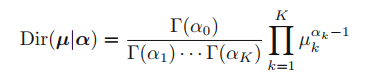
likelihood는 아래와 같다.
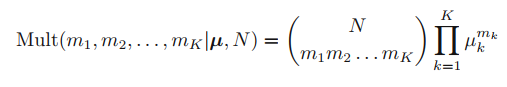
위의 두 가지를 곱해서 나온, 파라미터 {μ_(k)}에 대한 posterior distribution은 아래와 같다.
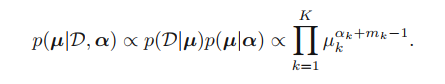
위의 수식에서 중간 term을 보면 p(D|μ)는 multinomial distribution이고
p(μ|α)는 Dirichlet distribution으로, 다시 Dirichlet distribution의 형태인걸 볼 수 있다.
고로 Dirichlet는 conjugate prior인 걸 확실하게 알 수 있으며, normalization coef.도 결정할 수 있다.

그럼 여기서 궁금한 것이.. multinomial disribution과 Dirichlet distribution의 차이는??
아래가 multinomial인데... 위의 dirichlet와 비교해보면 pi (product) 뒤에 나오는 μ_(k)위의 지수가...

multinomial은 m_(k) / 그리고 dirichlet는 α_(k)+m_(k)-1 인 차이밖에 없음을 알 수 있다.
beta prior를 가진 binomial distribution에서 봤던 것 처럼, dirichlet prior에서의 파라미터 α_(k)들은 x_(k)=1가 True인 애들의 (즉, 유효한) 개수들로 생각할 수 있다.

위의 그림에서도 볼 수 있듯이, dirichlet는 peak이 3개이거나 / 아예 없거나 / 1개 뿐이거나 한 경우만 가능하다.
즉, peak이 2개인 경우가 없는데, 이게 디리클레 분포의 한계이다. (parametric distribution들의 한계이기도 하다. 자신이 그릴 수 없는 shape들은 못함)
요약하자면 베르누이와 베타는 x가 scalar 값이다.
멀티노미얼과 디리클레는 변수가 여러개이다.
'Machine Learning > PRML' 카테고리의 다른 글
| [PRML] 8. Graphical Models (0) | 2021.06.06 |
|---|---|
| [PRML] 6.4.1~6.4.4 Kernel Methods (0) | 2021.04.04 |
| [PRML] 4.1.6 ~ 4.2.4. (0) | 2021.01.03 |
| [PRML] 2.4~2.5 (0) | 2020.10.25 |
| Mathematical Notations of Machine Learning (0) | 2018.11.11 |



