| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 해외취업컨퍼런스
- #체험수업
- CommunicateWiththeWorld
- #Ringle
- 뉴노멀챌린지
- 영어회화
- 영어공부
- #영어발음교정
- 링글리뷰
- 오피스밋업
- #nlp
- #영어공부
- 링글커리어
- 영어시험
- 소통챌린지
- 링글
- Ringle
- 강동구장어맛집
- 장어랑고기같이
- 둔촌역장어
- #링글
- #링글후기
- 영어로전세계와소통하기
- #직장인영어
- 스몰토크
- 영어공부법
- 링글경험담
- 화상영어
- 성내동장어
- 총각네장어
- Today
- Total
Soohyun’s Machine-learning
[PRML] 4.1.6 ~ 4.2.4. 본문
| 4.1.6. Fisher's discriminant for multiple classes |
앞서 본 2개 클래스의 Fisher discriminat 판별식 generalization을 보고자 한다.
여기서는 input space인 D가 클래스 개수인 K보다 크다고 가정하고 간다.
input space인 D를 낮은 차원으로 변환하는 식 (bias는 없다.)

weight vectors w_k는 위의 식의 matrix W의 column이다. 이 matrix W의 컬럼의 개수는 D' 개이며, 마찬가지로 input space D보다 작다.
K개의 클래스가 있을 때의, within-class의 covariance matrix S_W는 아래와 같이 정의된다.

여기서 S_k와 m_k는 각각 아래와 같이 정의된다.


가장 마지막 수식에서 N_k는 클래스 C_k의 패턴 개수이다.
※ 이전 class가 2개일 경우의 S_w 공식(하단 4.28)을 보면, 클래스가 K개라 전체 summation이 붙었을 뿐 동일한 수식임을 알 수 있다.

between-class covariance matrix를 구하기 위해, 우선 아래와 같이 전체 covariance matrix의 총합 S_T를 보자.

N : 전체 샘플의 개수
m : 전체의 평균
S_T를 풀어보면.. 아래와 같은 수식이 나온다.

위의 수식에서 첫번째 텀이 S_W이고, 뒤의 텀이 S_B이다.
(S_W는 내부를 체크하므로, 내부의 각 포인트 x과 평균 m간의 거리를 체크하고,
S_B는 분포간의 거리를 체크하므로, 현재 클래스 m_k와 전체 데이터셋 평균 m간의 거리를 체크한다.)
때문에 총 합 S_T에서 S_W를 제외하면, 나머지 S_B가 나온다.

이 S_B는 K개의 매트릭스들의 합인데, 두 벡터간의 outer product는 랭크가 1이 되게 된다.
또한 수식 (4.44)에서의 제약으로 인해, K-1개의 매트릭스만이 independent하며, 이 말은 곧, K개의 features에서 자를 수 있는 판별식의 개수는 K-1개라는 뜻이다. (projection 된 건 K-1개의 columns의 eigenvectors의 span일 것이므로..)
즉, K-1이 '가능한' 최대치이다.

지금까지 정의한 covariance matrices S_T, S_W, S_B는 모두 input space인 x-space에서 정의된다.
이 x-space의 matrices를 D' 차원의 y-space에서 다시 정의해보자.

S_W 수식(4.47)과 S_B 수식(4.48)을 살펴보면, S_W는 summation이 1개가 더 붙은걸 볼 수 있는데, 내부 class에 속하는 것들을 체크하기 때문이고, S_B는 각 class의 것을 체크하기 때문이다.
μ_k는 클래스 내부의 mean값이고, μ는 전체 데이터의 mean값이다.
scalar값이 커야하므로(?? 거리인 s_k?) between-class covariance S_B가 컸으면 좋겠고, within-class covariance S_W는 작았으면(데이터들끼리 똘똘 뭉쳐있는) 좋겠다.
그걸 측정하는 방법은 여러가지인데, 그 중 하나가 아래와 같다.

위의 수식이 criteria가 될 수 있는건, s_w와 s_b간의 covariance가 적어질수록 분포가 잘 떨어져 있다는 뜻이 되기 때문이다.
잘 떼어진 s_w와 s_b는 trace(대각합)를 했을때, 그 값이 클수록 projection을 잘 했다는 뜻이 되며,
(-> D'개의 가장 큰 eigenvalues를 잘 찾았다 ^-^*)
그 값이 작을수록 projection을 잘 못했다(-_-)는 뜻이기 때문이다.
PCA가 variance를 최대화하는 축을 찾아서(!!!), projection을 하는 것과 같은 이유이다. (일종의 standardization 과정. 잘 projection된 데이터가 때깔도 좋.. 나?)
위의 공식을 다시 Project matrix W의 explicit한 function 으로 적어보면 아래와 같은 공식이 나온다.

목적은 J 함수를 maximize하는 w를 찾는 것이다.
projection을 할 때, K-1로 하는 이유는,
(.. 그치만 아직도 이 방법론이 LDA인지 PCA인지 헷갈린다.
LDA는 데이터를 1차원 낮춘 다음, 선형 분류를 가장 잘 되게하는 선들을 찾는 것인데,
PCA는 데이터의 분포를 최대화하는 축을 찾아서 거기에 projection하는 것이기 때문에...
그냥 여기에서 dimensionality reduction을 썼다- 정도로 생각하쟈=_=...)
| 4.1.7 The Perceptron Algorithm |

phi (') : basis 또는 feature vector로 하단의 bias component를 갖고 있다.

f(') : nonlinear function 또는 activation function
여기서는 step function을 썼다.

또한 이것도 이진 분류긴 하지만, 이번에는 t=1인 경우 클래스 C1로, t=-1인 경우 클래스 C2로 구분한다. (더 깔끔하게 떨어진다고 한다.)
퍼셉트론 알고리즘 역시도 w를 구하는 것이 메인 목표이며, 이 w를 구하기 위한 perceptron criterion은 아래와 같다.


W_transpose * Phi(X_n) == 0일 경우는 hyperplane, 즉, 결정 경계가 된다.
Stochastic Gradient Descent (SGD)를 사용해서 w를 수정해주자.

퍼셉트론이 동작하는 방식은..

위의 그림에서 축은 Φ(x)를 사용해 얻은 축(Φ1, Φ2)이다. (2차원이므로)
첫번째 그림에서의 검은 선은 w값으로 만들어진 최초의 결정 경계이며, 이를 중심으로 오분류된 데이터들과의 거리를 측정한다. 녹색 동그라미가 오분류된 데이터이며, 이로 인해서
두번째 그림에서의 검은 선은 조금 더 붉은색 쪽으로 세워진 걸 볼 수 있다.
왼쪽 하단 그림에서 또 오분류된 녹색 동그라미가 체크되고, 가장 마지막 그림에서 검은 선은 파랑과 빨강을 완벽하게 나누도록 조정되었다.
이렇게 에러를 줄여나가는, 조정 과정은 아래의 식으로 확인할 수 있다.

Perceptron Convergence Theorem (퍼셉트론 수렴 법칙)
해법이 있을 때, 퍼셉트론은 유한한 횟수만큼 반복하면 그 해법을 찾을 수 있다는 법칙.
하지만 두 가지가 문제가 있는데...
1) 수렴되기까지의 횟수가 몇 번인지 알기가 어렵다는 점
2) 이게 linearly separable한 데이터인지 아니면 수렴이 느린것인지를 알 수 없다는 점
특히 2)번의 linearly separable하지 않을 경우, 퍼셉트론으로는 해당 데이터를 갖고 수렴하는 걸 볼 수가 없다...
또한 퍼셉트론의 결과물은 확률값이 아니고, 3개 이상의 클래스들로 쉽게 generalize할 수도 없다.
가장 큰 한계점은 고정된 basis functions의 linear combinations라는 점이다.
| 4.2 Probabilistic Generative Models |

- 사전 확률 (prior) p(C_k)




independent and identical distribution
2개의 클래스를 가정, 첫번째 클래스 C1을 얻기 위해서 베이즈 룰을 사용한 posterior probability는 아래의 식과 같다.

아래는 로지스틱 시그모이드 함수이다.

Q. 어떻게 (4.58)이 (4.59)가 되나용?

시그모이드는 말 그대로 S 모양이기 때문이고, 가끔 squashing function이라 부르기도 한다. 전체를 0~1사이의 값으로 squash 해주기 때문이다.
이 함수는 아래의 symmetry property를 만족하며,
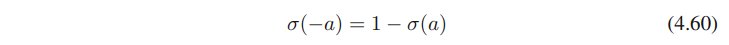
로지스틱 시그모이드 함수의 역(logit 함수)은 아래와 같이 주어진다.

이 logit 함수는 (2 클래스일 경우) 아래 수식 확률들의 비율(ratio)의 log를 대표하는데, log odds라고도 한다.
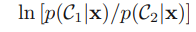
이름이 log odds라고 하는 이유는, 성공 확률 p와 실패 확률 (1-p)에 대한 odds가 p/(1-p)이므로, 여기에 log를 붙인 것과 같아서 그렇다고 한다.
이런 형태로 가장 첫번째로 보았던 아래 수식.. (4.57)을

3개 이상의 K로 일반화를 해보면 아래의 식이 되는데, 이를 generalized linear model 이라고 한다.

이 수식을 normalized exponential 또는 softmax function이라고 한다.
softmax의 어원은.. max 함수에 대한 smooth - 모든 점에서 미분 가능한 - 버전이라 그렇다고 한다 (@@.. 우왕)
위의 a_k는 아래와 같이 정의된다.

2개의 classes에서는 sigmoid로 분류, k개의 classes에서는 softmax로 분류
| 4.2.1 Continuous inputs |
우선 class-conditional density가 Gaussian이라고 가정하며, 모든 클래스가 같은 covariance matrix를 공유한다고 가정한다.
클래스 C_k에 대한 density 수식은 아래와 같다.

2개의 클래스라고 가정하고 보면 아래의 수식을 얻을 수 있다.

위의 수식은 (4.57)과 (4.58)에서 나왔는데


(4.65)가 (4.68)을 만족하게 할려면, w와 w_0는 아래와 같아야 한다.

여기에서 x에 대한 quadratic terms가 사라진 걸 볼 수 있는데, covariance matrices가 모두 동일하기 때문이다.
(이차항의 계수가 부호만 다르고 크기가 같아 약분되어서 그렇다-.... 고 한다.)
이 때문에 x에 대해서 linear function이 된다.

공분산이 같아서 모양이 같고, 위치만 다르므로 이를 분할하는 경계면은 직선이다.
위의 그림은 2-클래스 문제여서, 중간 위치에서 클래스가 나누어지는데... K클래스 문제로 확장을 해보면..


위의 두 식을 일반화 해보면.. K 클래스 문제를 풀 수 있다.

이는 공분산이 클래스마다 모두 같아서 이차텀이 사라졌기에 linear model로 된거고
만약 공분산이 클래스마다 다르다면 아래 그림처럼 경계면이 곡선이 될 수도 있다.

'Machine Learning > PRML' 카테고리의 다른 글
| [PRML] 8. Graphical Models (0) | 2021.06.06 |
|---|---|
| [PRML] 6.4.1~6.4.4 Kernel Methods (0) | 2021.04.04 |
| [PRML] 2.4~2.5 (0) | 2020.10.25 |
| [PRML] 2.1~2.2.1 Probability Distributions (0) | 2020.07.26 |
| Mathematical Notations of Machine Learning (0) | 2018.11.11 |




