| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 소통챌린지
- 오피스밋업
- #링글후기
- 링글커리어
- 영어로전세계와소통하기
- 스몰토크
- 강동구장어맛집
- 장어랑고기같이
- #링글
- 영어회화
- 영어시험
- 화상영어
- 영어공부
- #영어공부
- #체험수업
- Ringle
- 해외취업컨퍼런스
- 링글경험담
- #직장인영어
- #nlp
- 뉴노멀챌린지
- CommunicateWiththeWorld
- #영어발음교정
- 총각네장어
- 영어공부법
- 링글리뷰
- 링글
- #Ringle
- 성내동장어
- 둔촌역장어
- Today
- Total
Soohyun’s Machine-learning
[PRML] 2.4~2.5 본문
| 2.4 The Exponential Family |
2챕터 안에서 지금까지 배운 내용들은 모두 exponential family라고 불리는 분포 클래스의 세부 예시들이었다.
이름답게 이 패밀리의 members는 공통적되는 특성들이 있다.
데이터 x에 대한 분포의 exponential family는 아래 형태처럼, 분포의 세트로 정의된다.

x : scalar or vector
η (eta) : natural parameters (분포가 내재하고 있는 파라미터들 : e.g.) mean & variance in Gaussian)
u(x) : x의 어떤 함수
g(η) : 계수로 생각하면 되는 어떤 함수, 아래 (2.195) 수식을 만족하는지를 체크하여,
분포가 normalize 된 상태인지를 확인한다.

x가 discrete할 경우, integral은 summation으로 대체한다.
이제 이 챕터 전반부에서 봤던 몇몇 분포들이 '정말' exponential family의 멤버인지 보자.
|
Bernoulli distribution  |
먼저 베르누이 분포, 오른쪽을 exponential of the logarithm으로 표현해보면 아래와 같은 수식을 얻는다.

여기서 마지막 부분을 2.194의 오른쪽 항과 비교해보면,

그래서, 아래를 알 수 있다.

아래의 logistic sigmoid function에서, μ = σ(η)를 받아서 식을 μ에 대해서 풀면

베르누이 분포를 표준 형태인 (2.194)을 이용해서 풀어보면

아래 수식은 (2.199)로부터 얻어낼 수 있다

(2.200)의 형태를 (2.194)와 비교해서 보면, 아래의 사실들을 알아낼 수 있다. (단순 대입)

Multinomial distribution   |
위의 multinomial distribution을 (2.194)의 표준 표현식으로 나타내면



다시 (2.194)와 비교해보면 아래의 값들을 얻을 수 있다.

여기서 파라미터 eta_k는 파라미터 mu_k가 아래의 수식을 만족해야하기 때문에, 독립이 아니다.

이 제약 덕분에 mu_k에 대한 파라미터는 M-1개만 주어져도, 나머지 1개의 값은 자연히 알 수 있다.
때론 이 제약을 없애고 M-1 파라미터로만 나타내는게 좋을때도 있다. 이는 (2.209)의 mu_M을 삭제하는 것으로 나타낼 수 있다. 즉 mu_k는 1에서 M-1개까지만이고, M번째의 파라미터는 삭제하는 것.
이건 말보다 수식을 보는게 더 이해가 빠르다.

summation 표시 위의 M이 M-1로 바뀐 걸 알 수 있다.
(2.209)의 제약을 사용해서, 이 표현형의 multinomial distribution은

이걸로 알 수 있는 건

양쪽을 모두 k에 대해 sum하는 것으로 mu_k에 대해서 풀고, 그리고 다시 정리해보면 아래의 수식이 나온다. 이 수식이 softmax function (또는 normalized exponential)이다.

이 표현에서, multinomial distribution은 아래의 형태가 된다.
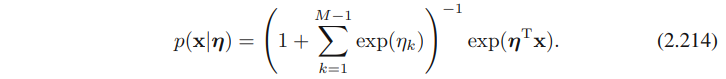
여기서 bold체의 eta는 1 ~ M-1까지의 값이다.

Gaussian distribution  |
마지막으로 가우시안 분포를 보자. (2.219)와 (2.194)를 비교해서 아래의 값을 얻을 수 있다.

| 2.4.1 Maximum likelihood and sufficient statistics |
일반적인 exponential family distribution의 파라미터 벡터 η를 측정하는데에, maximum likelihood를 사용해보자

위의 (2.195) 양쪽에 η에 대한 gradient를 취하면, 아래의 수식을 얻는다.

(2.194)와 (2.195)를 다시 사용해보면 아래의 수식이 나온다

그래서 얻게 된 결과는

u(x)의 covariance는 g(η)의 second derivatives로 표현될 수 있다.
그러므로, exponential family로부터 distribution을 normalize할 수 있다면, 항상 간단한 미분으로 그 순간을 찾을 수 있다.
이제 i.id 상태인 data 셋 X를 고려해보자.

이의 likelihood function은 아래와 같이 주어진다.

η에 대한 lnp(X|η)의 gradient를 0으로 세팅하면, maximum likelihood estimator인 η_(ML)에 의해 충족되는 아래와 같은 condition을 얻는다.

데이터에 대한 maximum likelihood estimator를 위한 솔루션은, (2.194)의 sufficient statistic (충분통계량)으로 불리우는 아래 term을 통과하는 것이다. (모든 데이터셋을 저장할 필요는 없고, 이 충분 통계량만 갖고 있으면 된다.)

베르누이 분포에서 함수 u(x)는 단지 x에 의해서 주어지고, 우리는 데이터 포인트들 {xn}의 합만 저장하면 된다.
가우시안의 경우는 아래와 같으므로, {xn}의 합과 {xn^2}의 합만 저장하면 된다.

만약에 N이 무한대로 가면, (2.228)의 오른쪽 항은 Ε[u(x)]가 되며, (2.226)과의 비교를 통해 limit η_(ML)은 η의 실제 값과 같게 된다.
| 2.4.2 Conjugate priors |
일반적으로, 주어진 확률 분포 p(x|η)에서, 우린 likelihood function과 conjugate한 prior p(η)를 찾을 수 있다. posterior distribution은 prior와 동일한 functional form을 갖는다.
exponential family의 어떤 멤버라도 아래와 같이 쓸 수 있는 형태의 conjugate prior가 존재한다.

f (X , v)은 normalization coefficient이다. g(η)는 (2.194)에서 본 것과 동일한 function이다.
g(η) : 계수로 생각하면 되는 어떤 함수, 수식을 만족하는지를 체크하여, 분포가 normalize 된 상태인지를 확인한다.
이게 진짜로 conjugate인지 보기 위해, prior (2.229)와 (2.227)을 곱해서, 아래와 같은 posterior distribution을 얻을 수 있다.

위의 prior, 그러니까 (2.229)와 동일한 형태인 것을 볼 수 있고, conjugacy가 있다고 볼 수 있다.
(더 이후에 파라미터 v 가 prior에 있는 pseudo-observations의 유효 숫자처럼 interpreted 될 수 있음을 볼 것이다. 그리고 각각은 X에 의해 주어진 u(x)의 충분 통계량이다. )
| 2.4.3 Noninformative priors |
이전의 prior들은 informative prior로 variable에 대한 사전 정보가 있다. 여기에서 볼 noninformative prior는 이 사전 정보가 없다. 이 prior의 쉬운 예로는 uniform distribution이 있다.
파라미터 λ에 의해 영향을 받는 분포 p(x|λ)를 보면, p(λ)를 상수로 하는것이 적합한 prior일 것이다. 만약 λ가 K개의 states를 가진 discrete variable이라면, 각 state를 1/K로 심플하게 세팅하는 것이다.
하지만 continuous parameters 일 경우, 이런식의 접근법에 두 가지 문제점이 생긴다.
1) 만약 λ의 domain이 unbounded하다면, prior distribution은 제대로 normalized 할 수 없다. λ에 대한 적분이 발산하기 때문이다. 이런 priors를 improper하다고 한다. 실제론, improper priors도 상응하는 posterior distribution이 proper할 경우엔, 종종 사용된다. 잘 normalize 될 수 있다는 뜻이기에.
(예시로, 가우시안 분포의 mean에 uniform prior distribution을 놓으면, posterior distribution의 mean에 적어도 한 개의 데이터 포인트라도 관측된다면 이는 proper가 된다.)
2) 다른 문제점은 (1.27)에서 variables의 nonlinear change 때의 probability density의 transformation behavior로부터 발생한다.

만약 함수 h (λ)가 상수이고, variables을 λ = η^2로 바꾸면, h_hat(η) = h (η^2) 역시 상수다.
그러나, 만약 density p_λ (λ) 도 상수이길 선택하면,

그러므로 η에 대한 density는 (1.27)에서 (2.231)로 주어진다.
그러므로 η에 대한 density는 상수가 될 수 없다.
이 문제는 maximum likelihood를 사용할 때는 발생하지 않는다. likelihood function p (x|λ)는 λ에 대한 심플 함수이므로, 얼마든지 편리하게 parameterization을 할 수 있다.
하지만 만약, prior distribution을 상수로 선택하면, 반드시 파라미터들을 적합하게 표현할 수 있는 방법을 써야 한다.
여기, noninformative priors에 대한 두 가지 간단한 예시들을 보자.
density가 아래의 형태를 취한다면
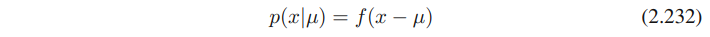
파라미터 μ는 location parameter이다. 이 family of densities는 translation invariance를 설명한다.
Q. translation invariance가 뭐임..
만약 x를 쉬프트하는 걸 x_hat = x + c로 하면,

여기서 μ_hat = μ + c 이다.
고로 우리는 density가 새로운 variable에서도 원래의 것과 같은 형태를 취한다는 것을 볼 수 있고, density는 origin의 선택으로부터 독립적이다. (??)
그럼 이 translation invariance property를 반영할 수 있는 prior distribution 을 선택하고 싶어지니, interval A ≤ μ ≤ B에 shifted interval A-c ≤ μ ≤ B-c 처럼, 동일한 probability mass를 할당하는 prior를 선택하도록 한다.
이는 아래 수식과 같은 의미인데, A와 B 사이의 모든 값을 갖고 있어야 하기 때문이고,

(2.234)의 가장 왼쪽과 가장 오른쪽 부분을 통해 아래와 같은 식을 얻을 수 있는데

이는 p(μ)가 상수라는 것을 암시한다.
location parameter의 한 예는 가우시안 분포의 mean일 것이다. 이 경우 μ에 대한 conjugate prior distribution은 아래와 같다.

noninformative prior는 아래를 취함으로써 얻을 수 있다.

(2.141)과 (2.142)로부터 μ에 대한 posterior distribution을 제공한다.
(여기서 μ는 이전의 것들은 사라진다)

(2.142)처럼 아래와 같은 형태의 density를 생각해보자.

여기서 알아둬야 할 것은 제공된 f(x) normalized density는 올바르게 normalized 되었다는 것이다.
파라미터 σ는 scale parameter로 알려져있다. 그리고 density는 sca;e invariance를 설명한다. 왜냐하면 x를 상수로 스케일링해서 x_hat = cx 므로,
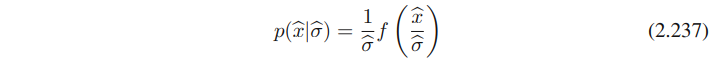
이 transformation은 scale의 변화에 상응한다. (만약 x가 길이라면 미터에서 킬로미터로 바뀌는 것) 그리고 이 scale invariance를 반영하는 prior distribution을 선택하고 싶다.
만약 우리가 interval A ≤ σ ≤ B, 그리고 scaled interval A/c ≤ σ ≤ B/c, 그리고 prior는 이 두 인터벌들에 대해 동일한 probability를 할당해야 할 것이다.

이는 반드시 A와 B의 선택들을 갖고 있어야 하기 때문에,

그래서 아래와 같이 된다.

여기서 알아두어야 할 점은, 이는 0과 무한대 사이라서 분포의 적분이 발산해버리므로, improper prior라는 것이다.
densities에 transformation rule (1.27)을 사용하면, p(ln σ)가 상수인걸 볼 수 있다.

그러므로, prior를 위해선 범위가 1과 10 사이든, 10과 100 사이든 동일한 probability mass를 사용해야 한다.
scale parameter의 예는, 가우시안 분포에서 location parameter μ를 취하고 난 다음의 standard deviation σ 일 것이다. 왜냐면

이전에 논한 바 있듯이 precision λ = 1/(σ^2)를 쓰는 것이 σ 자체를 쓰는 것보다 편하다.
densities에 transformation rule을 사용하는 것으로, p(σ) ∝ 1/σ 는 p(λ) ∝ 1/λ 형태의 λ에 관한 분포에 상응한다
λ에 대한 conjugate prior는, (2.146)처럼 주어진 gamma distribution인것도 봤다.
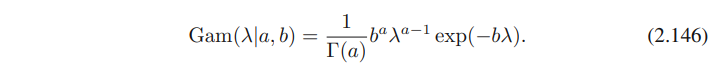
noninformative prior는 a0 = b0 = 0처럼 특별한 케이스로부터 얻을 수 있다.
아래의 (2.150)과 (2.151)을, λ의 posterior distribution에 대해 분석해본다면, a0 = b0 = 0임을 볼 수 있을 것이다. 이는 posterior는 데이터로부터 발생하는 것에만 의존한다. (prior로부터는 의존하지 않음)

| 2.5 Nonparametric methods |
지금까지 살펴본 애들은 density modeling을 하기 위한 parametric approach였고, 여기엔 한계가 있다.
아래의 그림처럼 multimodal한 데이터같은 경우, Gaussian distribution의 관점으로는 절대 체크할 수 없다. (Gaussian은 unimodal하므로)
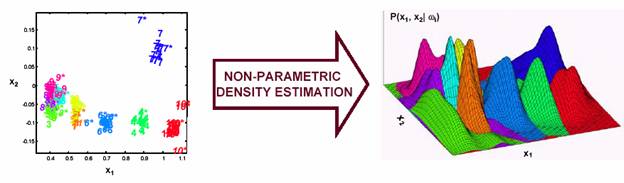
여기에선 density estimation을 위한 nonparametric approaches를 살펴볼 것이다. parametric approach에 비해 더 적은 수의 assumptions가 개입되며, simple frequentist methods에 중점을 둘 것이다.
density estimation을 위한 히스토그램 방법을 살펴보자.
여기선 histogram density models의 특징들을 (이전보다) 더 깊게 살펴볼 것이고, 하나의 continuous variable x의 케이스에 집중한다.
표준 히스토그램은 심플하게 x를 너비 Δi의 bins로 나누고, 관측된 x의 개수 ni를 bin i에 담는다. 이 count를 normalized probability density로 바꾸기 위해, 심플하게 너비 Δi 를 가진 총 N개의 관측치로 분리한다.
각 bin의 probability values를 얻어내는 공식은 아래와 같다.

pi : 하나에 대한 density probability value
Δi : 구간의 크기 (width of each bin)
ni : 해당 구간의 샘플 개수
이 p(x)의 적분은 1이 된다.
이걸로 density p(x)를 위한 모델을 얻는데, 각 bin의 너비에 따른 상수이며, 종종 같은 width Δi = Δ를 갖는다.

density estimation의 한 예시. 여기서 데이터는 녹색 선(mixture of two Gaussian)을 따라 그려진다.
서로 다른 bin의 크기에 따른 히스토그램 density estimation을 볼 수 있다. Δ는 매우 작은걸 알 수 있고, 실제 데이터셋이 그린 선, 녹색 선 바깥으로 많이 삐져나간 부분들(모델)도 볼 수 있다.
만약 Δ가 맨 아래의 히스토그램처럼 너무 크면, 모델의 결과가 너무 smooth하고, bimodal 특징을 잡아내는데에 실패한 걸 볼 수 있다.
여기서 최선의 결과는 중간의 값인데, bimodal도 잘 보이고, 바깥으로 삐져나간 모델의 부분도 적다.
원칙적으로, 히스토그램 density model은 bin의 엣지 위치를 어떻게 선택할 것이냐에 영향을 받지만, Δ의 값보다 일반적으로 덜 눈에 띈다.
알아두어야 할 것은, 히스토그램 방법이 가진 특성 중 하나는, 한 번 히스토그램이 계산되고 나면, 데이터셋은 버리기 때문에, 큰 데이터셋을 다룰 때에는 좋은 점이 있다. 그리고 히스토그램 접근법은 만약 데이터 포인트들이 순차적으로 도착한다면, 쉽게 응용된다.(???)
실전에선, 히스토그램은 데이터를 빠르게 visualization하는 방법이지만, 대부분의 density estimation 응용법에 맞지 않다.
명백한 문제 하나는 estimated density가 bin의 엣지 때문에 discontinuous하다는 것이며, 다른 주요 한계점으로는 dimensionality 관련한 scaling이다. D-dimensional space에 있는 각 variable을 M개의 bins로 나누면, bins의 총 개수는 M^(D)가 된다 (...) 너무 high-dim이라 local prob. density의 의미있는 측정을 하기 매우 어렵다.
그럼에도 이 접근법은 두 개의 중요한 것을 가르쳐준다.
1) 특정한 위치의 probability density를 측정할 때, 그 위치의 some local neighborhood안에 있는 데이터 포인트들을 감안해야 한다는 점. locality의 컨셉은 distance measure의 어떤 form을 가정하는데, 여기선 유클리디언 distance가 있다.
히스토그램에서, 이 neighborhood 특성은 bin에 의해 정의된다. 거기엔 local region의 공간적 범위를 묘사하는 natural '스무딩' 파라미터가 있는데, 이 경우엔 bin width이다.
2) 스무딩 파라미터는 좋은 결과를 얻기 위해, 반드시 너무 크지 않아야 하고, 너무 작지도 않아야 한다.
이는 폴리노미얼 커브 피딩에서 모델 복잡도를 선택하던 때를 기억나게 하며, 이런 인사이트를 갖고 이제 많이 사용되는 density estimation을 위한 nonparametric technique를 보자.
| 2.5.1 Kernel density estimators |
어떤 D-dimensional space에 있는, 알려지지 않은 probability density p (x)로부터 데이터가 그려진다고 가정해보자.
여기서 유클리디언 distance를 써서, p(x)의 값을 추정해보자.
x를 담고 있는 작은 공간 R을 생각해보자. probability mass는 이 공간과 관련되어 있으며, 아래처럼 주어진다.

p (x)로부터 그려졌고, N 관측치로 이루어진 데이터셋을 생각해보자.
각 데이터 포인트는 R 에 떨어진 probability P 를 갖고 있기에, 총 포인트 개수 K 는 binomial distribution을 따라 R 안에 퍼져 있다.

아래 (2.11)을 사용해서, 공간 안에 떨어진 포인트들의 평균 fraction은 E[K / N ] = P 임을 알 수 있다.

비슷하게 (2.12)을 사용해서 이 mean 주변의 variance가 var[K / N ] = P (1 - P )/N 인 것도 알 수 있다.
N이 크면, 이 분포는 mean 주변에서 날카롭게 peaked한 모습을 보인다. 그러므로

그러나 만약, 공간 R이 충분히 작고, 공간의 probabilty density p(x)가 얼추 상수라면, 아래처럼 볼 수도 있다.

V : volumne of R
위의 (2.244)와 (2.245)를 합쳐서, 아래와 같은 형태로 density estimate를 얻을 수 있다.

(2.246)의 타당성은 두 개의 상반된 assumptions에 달려있다.
1) 공간 R이 충분히 작고, 공간의 density는 얼추 상수이며, 충분히 크지는 않아야 한다. (density의 값과 관련)
2) 데이터 포인트 K들은 공간안에 binomial distribution에 충분하게 있어야 한다. (sharply peaked)
위의 수식 (2.246)의 결과를 두 가지 다른 방법으로 탐색할 수 있다.
K를 고정하고, V의 값을 탐색하거나 (KNN처럼), V를 고정하고 K를 데이터로부터 결정하는 것이다 (Kernel approach)
- 이는 KNN density estimator와 kernel density estimator는 제공된 V가 N에 알맞게 축소되고, K가 N과 함께 성장하면, N이 무한대로 갈 때, true probability density에 수렴되는 걸로 나타난다.
Kernel method를 보자.
공간 R은 포인트 x를 중심으로 하는 작은 하이퍼 큐브이고, 이것의 probability density를 결정해보자.
이 공간안에 들어가 있는 포인트들의 개수 K를 세기 위해, 아래처럼 함수를 정의하는 게 편리하다.

이 함수는 origin을 중심으로 하는 unit cube를 나타낸다.
함수 k(u)는 kernel function의 예시이며, 이 context에선 Parzen window라고 불린다.
(2.247)로부터 수량 k ( (x - xn)/h ) 는 하나일 수 있다. 만약 데이터 포인트 xn이 x를 중심으로 하는 side h 의 큐브 안에 있고, 나머지는 0이라면.
이 큐브안에 있는 총 데이터 포인트의 개수는 아래와 같다.

이 표현형을 (2.246)에 집어넣어 대체해보면, x에 대한 estimated density의 결과는 아래와 같다.

V = h ^(D) : D-dimensions를 가진 side h의 하이퍼 큐브의 볼륨
함수 k (u)의 대칭을 사용해, 이 수식을 다시 만들어보자.
(2.249)는 히스토그램 방식과 비슷한 문제가 있다. artificial discontinuous, 히스토그램의 bin의 엣지가 이 경우에는 큐브의 바운더리가 된다.
smoother kernel function을 사용해서 smoother density model을 만들건데, Gaussian이 보편적인 선택이다.

h : standard deviation of the Gaussian components
이 density 모델은 각 데이터 포인트에 가우시안을 놓는 것으로 얻어낼 수 있고, 전체 데이터셋에 대해서도 이렇게 한다. 그리고 N으로 나누므로 density는 normalized 되어있는 것도 알 수 있다.

히스토그램의 경우처럼, 중간의 h가 가장 나음을 볼 수 있다.
(2.249)에 있는 k(u)는, 아래의 조건을 만족하는 다른 커널 함수로 선택할 수도 있다.

| 2.5.2 Nearest-neighbor methods |
위의 kernel density estimation의 문제점 하나는, 모든 커널에 대한 파라미터 h가 고정이라는데에 있다.
여기서는 다시 (2.246)으로 돌아가 V를 픽스하고 K를 결정하는 대신, K를 고정하고 V를 위한 적합한 값을 찾아내자.

density p(x)를 추정하기 위해, 포인트 x를 중심으로 하는 작은 구체를 생각하자.
정확한 K 데이터 포인트를 측정하기 위해, 구체의 반지름을 꾸준히 증가시킬거다.
여기선 위의 수식에서의 V를 결과 구체의 볼륨으로 본다.
이러한 테크닉을 KNN이라고 한다.

앞선 데이터와 같은 데이터를 사용한 결과이며, K의 수치가 파란색 선의 smoothing을 결정함을 볼 수 있다.
KNN에 의해 생성되는 모델은 true density model은 아니다. 전체 space의 적분은 여전히 발산하기 때문이다.
이 챕터는 density estimation을 위해 KNN을 적용하는 것을, classification 문제로 확장시켜보는 것으로 끝마칠까 한다.
이를 위해서, KNN density estimation technique을 각 class 별로 적용하고 Bayes' theorem을 사용한다.
각 클래스 C_k는 N_k개의 포인트로 이루어져 있으며, 전체 데이터 포인트는 N개이다. 그러므로 N_k를 모두 합한 값은 N이 된다. 만약 새로운 포인트 x를 classify하고 싶으면, x를 중심으로 하며 그들의 클래스와 관련없이 K개의 데이터 포인트를 가진 구체를 그리면 된다. 수식은 아래 (2.253)과 같다.

아래 그림의 내용은 majority class membership에 따라 포인트가 classify 된다는 내용.

오분류를 줄이고 싶다면, K_k/K의 가장 큰 값에 상응하는 가장 큰 posterior probability를 가진 테스트 포인트 x를 설정한 다음 체크 해보면 된다.
K=1인 케이스는 특별히 nearest-neighbor rule이라고 한다. 왜냐하면 테스트 포인트는 단순히 주변에 가장 가까운 포인트 클래스에 들어가기 때문이다.

위의 그림에서 K는 smoothing의 정도를 나타냄을 볼 수 있고, 큰 K일수록 영역도 크게 가져가는 것도 볼 수 있다.
nearest-neighbor (K=1) classifier의 흥미로운 특성 하나는, N이 무한대로 갈때 에러율은 optimal classifier의 최소 달성 가능한 에러율의 두 배를 절대로 넘지 않는다는 점이다. 다른말로 하나는 true class distributions을 쓴다는 거다. (one that uses the true class distributions)
nearest neighbors는 데이터셋에 대한 exhaustive search없이도 효과적인 편이지만, 그럼에도 kernel method 포함 이런 nonparametric methods는 여전히 극도로 제한적이다.
다른 한편으론, 분포의 모양새란 점에서 simple parametric methods도 매우 제한적임을 볼 수 있었다.
'Machine Learning > PRML' 카테고리의 다른 글
| [PRML] 8. Graphical Models (0) | 2021.06.06 |
|---|---|
| [PRML] 6.4.1~6.4.4 Kernel Methods (0) | 2021.04.04 |
| [PRML] 4.1.6 ~ 4.2.4. (0) | 2021.01.03 |
| [PRML] 2.1~2.2.1 Probability Distributions (0) | 2020.07.26 |
| Mathematical Notations of Machine Learning (0) | 2018.11.11 |



