| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 영어회화
- #영어발음교정
- 장어랑고기같이
- 소통챌린지
- 화상영어
- 강동구장어맛집
- CommunicateWiththeWorld
- 영어시험
- 둔촌역장어
- Ringle
- 해외취업컨퍼런스
- 링글
- 성내동장어
- #링글후기
- #링글
- 링글경험담
- 영어로전세계와소통하기
- 오피스밋업
- 링글커리어
- 뉴노멀챌린지
- 총각네장어
- #영어공부
- 스몰토크
- #Ringle
- #체험수업
- #nlp
- 링글리뷰
- 영어공부법
- 영어공부
- #직장인영어
- Today
- Total
Soohyun’s Machine-learning
[PRML] 8. Graphical Models 본문
Probabilistic Graphical Models
확률적 그래피컬 모델이 가진 속성들
1. 확률적 모델의 스트럭쳐를 보여줄 수 있는 간단한 방법을 제공하며 새로운 모델을 만드는데 동기부여가 될 수도 있다.
2. 모델의 속성들에 대한 인사이트(그래프를 검사하는걸로 얻어낼 수 있는, 조건부 독립 속성 conditional independence properties 포함) 를 제공한다.
3. 복잡한 연산, 복잡한 모델을 배워야 하고 추론을 해야한다.
그래프는 노드 nodes (버텍스, vertex/vertices)와 그걸 이어주는 링크 links (엣지 edges, 아크 arcs)로 구성되어 있다.

graphical models에서 각 노드는 확률 변수 random variable (or group of random variables)이며, 이 변수들 사이의 관계는 링크 link로 나타낸다.
그래프는 모든 확률 변수간의 joint distribution을 보여주며, 이는 각 변수들의 subset에 의존하는 factors의 곱으로 분해할 수 있다.
- 베이지안 네트워크 Bayesian Networks (directed graphical models) : 그래프의 링크가 방향성이 있다.
ㄴ 방향성이 있는 그래프는 확률 변수들간의 인과관계를 표현하는데에 좋다
- 마코프 랜덤 필드 Markov Random Fields (undirected graphical models) : 링크가 방향성이 없다.
ㄴ 방향성이 없는 그래프는 확률 변수들간의 약한 제약들을 표현하는데에 좀 더 낫다
추론 문제를 풀기 위해서는 directed / undirected graph를 factor graph로 바꾸면 좋다.
| 8.1 Bayesian Networks |
확률 분포 probability distributions 를 표현하기 위해 directed graphs를 사용해보자.
어떤 변수들 a,b,c에 대한 joint distribution p(a,b,c)가 있다. (여기서 변수들이 discrete / continuous 한지 어쩐지는 생각하지 않는다)

확률의 product rule에 의해서 위의 joint distribution은 아래처럼 다시 쓸 수 있다.
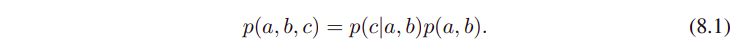
그리고 p(a,b) 부분을 더 분해해서 아래처럼 또 쓸 수 있다.

여기서 우측의 텀을 graphical models로 나타내면 아래 그림처럼 된다.

a는 어디에서도 오는 link가 없으므로 p(a)가 되고,
b는 a로부터 link가 오므로, p(b|a)가 된다. (여기서 a는 노드 b의 parent라고 할 수 있으며, b는 a의 child가 된다.)
마지막으로 c는 a와 b, 둘로부터 links를 받으므로 p(c|a,b)가 된다.
(8.2) 수식에서 재미있는 점은 좌측은 a,b,c 모두에 대해 표현방식이 같은데, 좌측은 a,b,c를 표현한게 다르다는 점이다. a,b,c의 순서를 바꾸거나 하면 다른 방식의 분해가 가능하고, 그러면 다른 graphical representation이 된다. 이건 나중에 알아보자.
Figure (8.1)을 K개 변수들 p(x1, ... ,x_(K)) 간의 joint distribution으로 확장해보자.
확률의 product rule에 의해 아래처럼 적을 수 있다.

위의 수식에서 우측을 보면, 모든 노드는 그보다 더 작은 노드로부터 links를 받는걸 볼 수 있다. 이런 그래프를 fully connected (FC)하다고 한다. 모든 노드 pairs간에 link가 존재하기 때문이다.
FC를 보았으니 이제 link가 absence 한 케이스도 보자.

위의 Figure (8.2) 그래프는 FC가 아님을 알 수 있다. x1과 x2간의 link가 없고, x2와 x7간의 링크도 없고, 이외에도 많은 노드들간의 링크가 존재하지 않기 때문이다.
위의 {x1, ... , x7} 그래프를 수식으로 나타내면 아래와 같다.
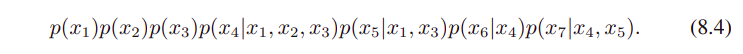
그래프에 의해 정의되는 joint distribution은 product로서 주어진다. 각 노드의 conditional distribution은 그래프에서 해당 노드의 parents 노드들에 conditioned하다. 따라서 K개의 노드들로 이루어진 그래프의 joint distribution은...
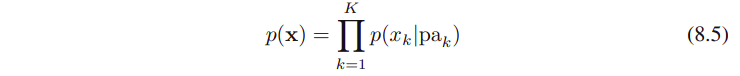
여기서 우측 텀의 pa_(k)는 x_(k)의 부모 노드들의 집합 x = {x1, ... ,x_(k)} 이다.
이 수식은 directed graphical model에서 joint distribution의 factorization 속성을 나타낸다.
방향성에 있는 그래프 directed graph 는 directed cycle이 반드시 없어야만 한다.
A -> B -> C -> A 이런식의 cycle이 없어야 한다는 뜻으로, 이런 그래프를 Directed Acyclic Graphs (DAGs)라고도 한다. 이는 어떤 노드도 그보다 낮은 노드로 향하는 link가 없다는 걸 나타낸다.
| 8.1.1 Example: 다항 회귀 Polynomial regression |
(1.2.6) Bayesian curve fitting에서 본 모델의 확률 변수 random variables는 다항 계수 polynomial coefficients w 벡터와 관측된 데이터 t = (t1 ... ,t_(N)).T 이다.
그리고 모델의 input data로 x = (x1, ... ,x_(N)).T 가 있고,
noise variance σ^2,
하이퍼파라미터 α (w에 대한 Gaussian prior의 precision)가 있다.
이들은 변수라기보다는 모델의 파라미터들이다.
지금은 확률 변수에만 집중해보자.
joint distribution은 prior p(w)와
N개의 조건부 분포 conditional distributions p(t_(n) | w) n = 1,...,N 이다.

하단의 Figure (8.3)은 이 joint distribution을 graphical model로 나타낸 것이다.

위의 그래프에서 볼 수 있듯이, t1~t_(N)까지의 모든 노드를 그려놓지는 않는다. ( dot 점들이 중간 부분을 줄였다는 표시 )
이를 더 compact하게 표현하는 것이 플레이트 plate 이다.
Figure (8.4)의 plate에서 N은 같은 종류의 노드들 N개를 나타낸다. 위의 Figure (8.3)을 Figure (8.4)로 더 간편하게 표시했다.

모델의 파라미터와 랜덤 변수 stochastic variables를 명시적으로 나타내는게 도움이 될 때도 있다. 그래서 수식 (8.6)을 다시 적어보면, 아래와 같이 나타낼 수 있다.
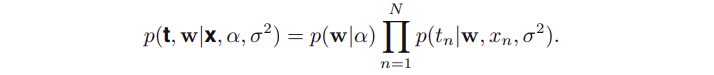
위의 수식처럼 명시적으로 나타난 애들도 graphical representation으로 나타내보자.
확률 변수 random variables는 동그랗지만 내부가 빈 원 ◎
deterministic parameters는 작고 속이 꽉 차있는 원 ● 으로 나타낼 것이다.
아래 Figure (8.5)에서 볼 수 있는 deterministic parameters : x_n, α, σ
random variables : {t_1, ... , t_n}, w

그리고 확률 변수 random variables 중에서 관측된 애들은 색깔이 들어간 원으로 나타낼 것이다.
그러므로 Figure (8.5)는 {t_1, ... ,t_n}이 관측된 변수라고 할 때 아래의 Figure (8.6)처럼 바뀌게 된다.
(w는 관측되지 않았기에 동일한 모습임을 다시 한 번 상기하자. 여기서 w는 잠재 변수 latent variable , hidden variable 의 예시이다.) -- 더 자세한 내용은 챕터 9와 챕터 12에서 하겠다.

관측된 t_n값을 갖고서 다항 계수 polynomial coefficient w의 사후 확률 posterior distribution을 evaluate할 수 있다.
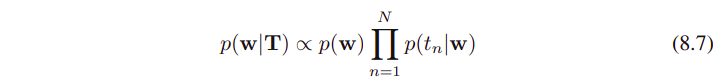
이 모델의 모든 확률 변수 random variables 의 joint distribution (deterministic parameters도 나타낸) 을 보면...

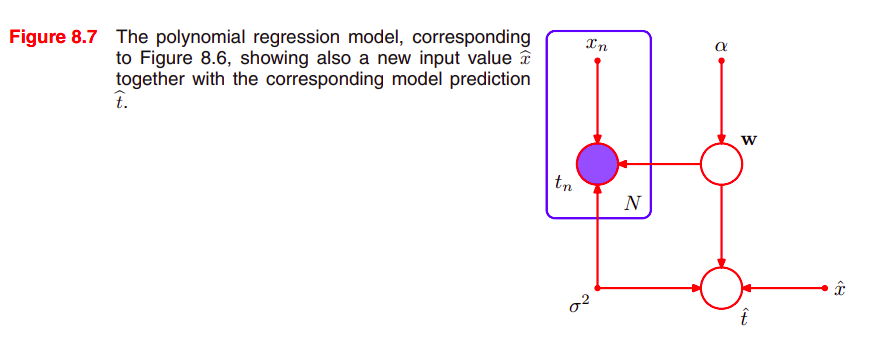
새로 들어온 input value인 t_hat에 대한 predictive distribution을, 확률의 sum rule로부터, 모델 파라미터 w를 통합하는 것으로 얻어낸다.

여기서 t의 확률 변수 random variables 를, 데이터셋에서 관찰된 특정한 값으로 암시적으로 설정한다.
| 8.1.2 Generative models |
ancestral sampling을 소개한다.
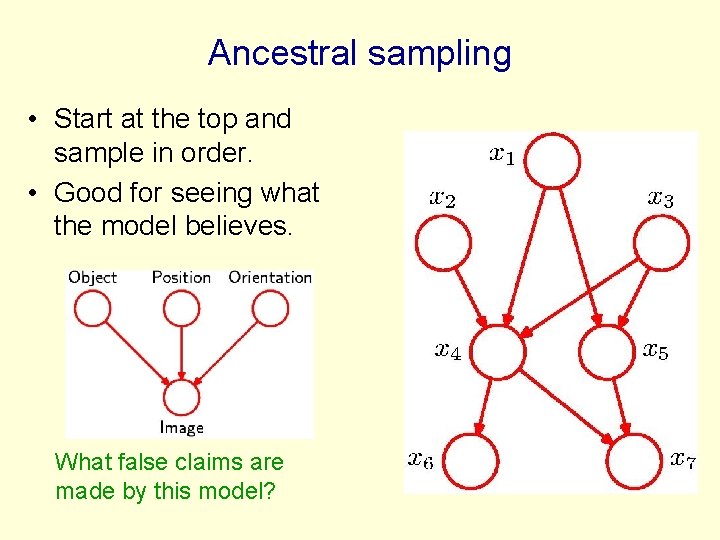
방향성 비순환 그래프 directed acyclic graph인 (8.5)를 따라 K개의 변수들에 대한 joint distribution p(x1, ... ,x_(k))를 생각해보자.
목표는 joint distribution으로부터
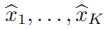
을 샘플링하는 것이다.
이를 위해서 가장 작은 수의 노드로부터 시작해서 분포 distribution p(x1) (== x1_hat) 을 샘플링해 나갈 것이다.
각 스테이지마다 조건부 확률 conditional distribution p(x_n | Pa_n)은 항상 샘플링이 가능하다. (parent variable이 있으므로)
마지막 변수 final variable x_(K)를 샘플링하면, joiny distribution으로부터 샘플링하는 목표가 달성된거다.
그리고 각 variables의 subset에 대응하는 marginal distribution으로부터 샘플링을 하기 위해서, 필요한 노드의 샘플들만 취하고 나머지는 무시할거다.
e.g.) 분포 p(x2, x4)에 대한 샘플을 얻기 위해서, 전체 joint distribution으로부터 샘플링을 하고, x2_hat, x4_hat의 값을 얻고, 2와 4번째 x가 아닌 나머지 값들은 포기한다.
확률 모델 probabilistic models의 실전으로, 보통 그래프에서 높은 값을 가진 (관측된) 노드를 터미널 노드 terminal nodes로 삼고, 낮은 값의 노드들을 대응하는 잠재 변수 latent variables로 한다.
잠재 변수 latent variables의 주요 역할 primary role은 관측된 변수들에 대한 복잡한 분포 complicated distribution을 허용하는 것이다. (간단한 conditional distributions로부터 모델을 설계하는 관점에서)
이걸 관측된 이미지 파일을 프로세싱하는 것에 대입해보면, object recognition 태스크에서, 관측된 데이터 포인트는 오브젝트의 하나의 이미지 (픽셀 숫자들 벡터) 라고 볼 수 있다. 잠재 변수 latent variables는 오브젝트의 위치 position와 방향성 orientations으로 해석될 수 있다. 목표는 오브젝트들에 대한 사후 분포 posterior distribution를 찾는 것이다.
이를 graphical model로 나타내보면 아래와 같다.

graphical model은 데이터가 생성 generate 된 casual process을 찾아낸다. 그래서 generative models이라고 불리기도 한다.
반대로 다항 회귀 polynomial regression은 generative model이 아닌데, 입력값과 관련된 probability distribution이 없기 때문이다. 적합한 prior distribution p(x)를 introducing하는 것으로 generative로 만들 수는 있지만, 더 복잡한 모델이 된다.
| 8.1.3 Discrete variables |
예전에 exponential family를 배운적이 있다. 이와 graphical models을 연계해서 유용하게 쓸 수 있다.

방향성 그래프 directed graph에서 부모-자식 노드 페어 parent-child pair의 관계가 conjugate하다면 특히 더 좋다.
예시를 보자.
부모-자식 노드가 Gaussian variables이고, discrete variables이다. 이 경우 복잡한 DAG (directed acyclic graphs)를 만들때, 계층적으로 확장할 수 있기 때문이다.
하나의 discrete variable x (K개의 가능한 states를 가진) 에 대한 확률 분포 p( x | μ )는 아래와 같이 주어진다.


이제 x1, x2의 두 개의 이산 변수 discrete variables (각각 K개의 states를 가진) 를 갖고 있다고 해보자.
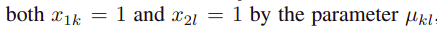
파라미터 mu_(kl)에 의한 각 값의 관측 확률 probability of observing 은 위와 같다.
x_(1k) : x1의 k번째 요소
x_(2l) : x2의 l번째 요소
joint distribution은 아래처럼 쓸 수 있다.

파라미터 mu_(kl)은 아래의 제약 사항을 만족시켜야 하기 때문에, 분포는 K^(2) - 1개의 파라미터들로 지배된다.

파라미터의 전체 숫자가 M개의 변수에 대한 어떤 joint distribution이기에, 변수의 개수 M은 지수적으로 exponentially 증가한다는 걸 알 수 있다.
product rule을 써서, x1에서 x_2로 가는 두 노드간의 joint distribution p(x1, x2)는 p(x2|x1)p(x1)의 형태를 한다는 걸 알 수 있다.
위의 Figure 8.9 (a)에서 볼 수 있으며, 변수의 개수는 K^(2) - 1 이다.
두 노드가 independent할 경우 link가 없고, 파라미터 개수는 2(K - 1) 이 된다. 이걸 M개의 independent discrete variables로 확장하면 파라미터 개수는 M(K - 1)개가 되어서, 변수의 개수만큼 선형적으로 증가함을 볼 수 있다.
이처럼 graphical 관점에서 볼 때, 그래프상에서 link를 없애는 것으로 파라미터의 개수를 줄일 수 있다. M개의 변수들을 가진 그래프가 fully connected라면 파라미터 개수는 K^(M) - 1이 된다. (링크가 없다면 위에서처럼 M(K - 1))
이제 아래 그림을 보자.

marginal distribution p(x1)은 K - 1개의 파라미터들을 필요로 한다.
위의 M개의 variables을 가진 체인은 K에 대해 quadratic하고, M에 대해서는 선형적으로 증가한다.
파라미터의 전체 개수는 K - 1 + (M - 1) K (K - 1)이라는 수식에서 볼 수 있듯이.
모델의 independent한 파라미터를 줄이는 다른 방법은 파라미터를 sharing하는 것이다. (typing of parameters라고도 함)
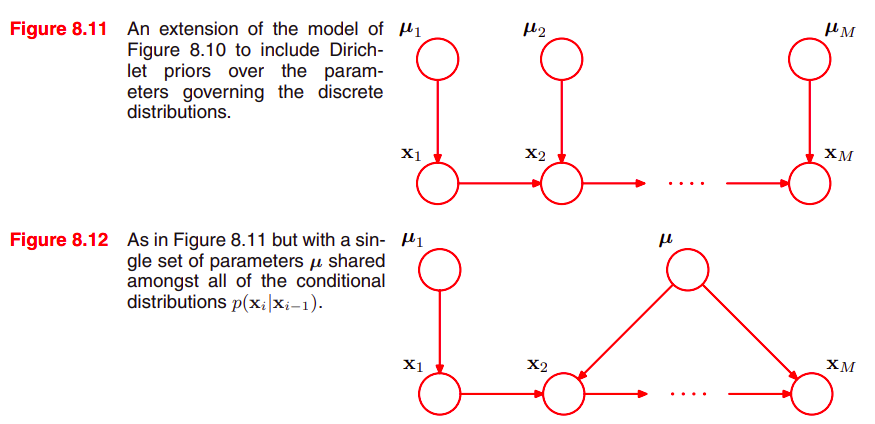
디리클레 사전 확률 Dirichler priors로 이산 변수에 대한 그래프를 베이지안 모델로 바꿔보겠다.
graphical 관점에서 각 노드는 Dirichlet distribution을 표현하는 추가적인 parent가 필요하다. 이는 Figure (8.11)에서 볼 수 있다.
이 모델은 conditional distribution을 제어하는 파라미터들을 연결한다.
파라미터의 개수가 지수적으로 증가하는 걸 제어하기 위한 다른 방법은 conditional probability values의 전체 테이블을 사용하는 게 아니라, conditional distribution을 위한 parameterized models을 사용하는 것이다.
아래의 Figure (8.13)을 보자.
모든 노드는 binary variables이다.

각 parent values x_i는 μ_i에 의해서 제어되며,
여기서 μ_i는 probability p(x_i = 1) 이다.
y의 parent nodes로는 M개의 x_i가 들어가지만...
2^(M) parent variables의 가능한 세팅들에 대한 확룰 p(y=1)를 나타내기 위해선,
conditional distribution p(y | x1, ... , x_m)은 2^(M)개의 파라미터가 필요하다. (지수적으로 파라미터가 증가한다.)
parent variables의 선형 컴비네이션 linear combination, 로지스틱 시그모이드 함수를 사용해서 conditional distribution을 심플하게 표현해보자.
그러면 아래와 같은 수식이 나온다.
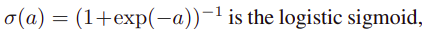
x : 추가 variable x_0와 함께 증강된 parent states의 (M + 1) 차원 벡터, 값은 전체를 합해서 1로 되게 되어있다.
e.g) [0,0,.... ,1, ..., 0,0]

이는 conditional distribution의 상당히 제한된 형태지만, 그래도 파라미터가 M에 선형적으로 증가한다. multivariate Gaussian에서 제한적인 형태의 공분산 행렬을 선택하는 것과 비슷하다. (e.g. diagonal matrix)
| 8.1.4 Linear-Gaussian models |
이전 섹션에서 DAG의 노드들을 표현하는 것으로 discrete variables에 대한 joint probability distributions를 만들어보았다.
여기서는 multivariate Gaussian이 linear-Gaussian model에 대응되는 directed graph로 어떻게 표현할 수 있는지를 보여준다.
널리 쓰이는 linear-Gaussian 모델은 PCA, factor analysis, 그리고 LDS등이다. (세부적인건 나중 챕터에서 보도록 한다.)
D개의 variables를 가진 directed acyclic graph를 생각해보자. (각 노드 i는 Gaussian distribution에서 하나의 continuous random variable x_i를 나타낸다.)
이 분포의 mean은 각 parents nodes pa_(i)의 state들의 linear combination이다.
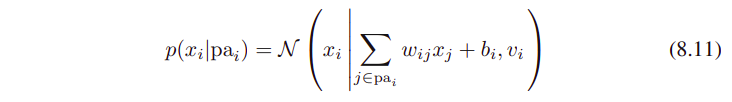
w_(ij)와 b_i는 mean을 제어하는 파라미터들이다.
v_i : x_i에 대한 conditional distribution의 분산 variance
joint distribution의 log는 그래서 모든 노드들에 대한 이런 conditionals의 product에 log를 취한 값이다.
이를 수식으로 나타내보면...

x = (x1, ... , x_(D)).T
const : indenpendent term of x
위의 수식을 보면 x 요소의 quadratic한 함수임을 볼 수 있고, 그래서 joint distribution p(x)는 multivariate Gaussian이 된다.
(distribution의 봉이 하나가 아니다.)
joint distribution에 대한 mean과 covariance는 아래 수식처럼 재귀적으로 결정한다.
각 x_i (부모 노드의 states에 conditional)는 수식 (8.11)처럼 Gaussian distribution이다.

(8.11)의 parents nodes부분인 Pa_(i)에 루트를 씌운 v_i (표준편차 standard deviation 같다)와 epsilon_i의 곱이 추가되었음을 볼 수 있다.
여기서 epsilon_i는 standard normal Gaussian (zero mean + unit variance) random variable이며,
아래의 수식들을 만족한다.
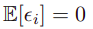

여기서 I_(ij)는 identity matrix의 i,j번째 요소
수식 (8.14)에 expectation을 취하면, 아래의 수식을 얻을 수 있다.

그래서 가장 작은 노드에서 시작해서 그래프 전체를 재귀적으로 돌려봄으로써, 하단의 요소를 찾아낼 수 있다. (여기서 각 노드는 그 parent node보다 값이 크다)
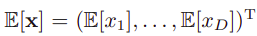
비슷하게, p(x)의 공분산 행렬 요소 i,j를 얻어내기 위해서, (8.14)와 (8.15)를 쓸 수 있다.

이제 2개의 극단적인 케이스들을 보자.
첫번째로 노드들 사이에 링크가 없고, D개의 독립된 노드만 있다고 가정한다.
이 경우 w_(ij) 파라미터가 없고, D개의 b_i와 D개의 v_i 파라미터들만 존재한다.
(8.15)와 (8.16)의 재귀적 관계에서, p(x)의 mean은 (b1, ... , b_(D)).T로 주어짐을 볼 수 있다.
그리고 공분산 행렬은 diag(v1, ... ,v_(D)) 형태이다. (diagonal matrix)
joint distribution은 2D 파라미터들의 총합을 갖고 있고 D개의 independent univariate Gaussian distribution의 세트를 나타낸다.
이제 모든 노드가 이어진 fully connected graph를 생각해보자. (물론 낮은 값을 가진 노드들이 parents)
행렬 w_(ij)는 그러면 i번째의 행에서 i - 1개의 엔트리를 가지며, 이 lower triangular matrix가 된다. (leading diagonal에는 엔트리가 없다.)
그러면 파라미터 w_(ij)의 총합은 D by D 행렬안에 있는 요소들의 D^(2) 숫자를 취하고, D를 빼고 (leading diagonal에는 없으므로), 그리고 다시 2를 나눠줌으로써 얻어낼 수 있다. D (D - 1) / 2 의 총합
공분산 행렬에 있는 independent parameters {w_(ij)}와 {v_i}의 총합은 그래서 D (D + 1) / 2가 된다. (일반적인 symmetric covariance matrix에 대응한다.)
중간 레벨의 복잡도를 가진 그래프는 일부 제약이 걸린 covariance matrices를 가진 joint Gaussian distributions에 대응한다.
아래 그림을 보자.
x1과 x3 사이에는 link가 없다.

(8.15)와 (8.16)의 재귀적 관계를 사용하면, joint distribution의 mean과 covariance는 아래와 같이 주어진다.
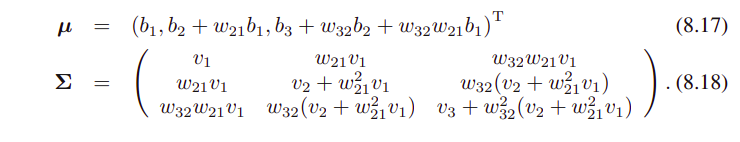
이 linear-Gaussian model을 multivariate Gaussian으로 확장해보면,
node i에 대한 conditional distribution은 아래와 같이 쓸 수 있다.

W_(ij) : matrix (whether square or nonsquare)
이 수식에서도 모든 변수들에 대한 joint distribution이 Gaussian임을 볼 수 있다.
여기까지 본 linear-Gaussian relationship의 세부 예시들은 conjugate prior들이다.
x와 mu 모두 Gaussian이며 그 결과도 Gaussian으로 나올 수 밖에 없다.
mu에 대한 분포의 mean은 prior를 조정하기 때문에 하이퍼 파라미터로 볼 수 있으며 (이 경우 hyperprior라고도 함), 이 값을 모를 경우 베이지안 관점에서 얻어낼 수 있다.
이런 구조는 어느 레벨의 계층적 베이지안 모델로든 확장할 수 있다.
'Machine Learning > PRML' 카테고리의 다른 글
| [PRML] 8.4 Inference in Graphical Models (0) | 2021.07.30 |
|---|---|
| [PRML] 6.4.1~6.4.4 Kernel Methods (0) | 2021.04.04 |
| [PRML] 4.1.6 ~ 4.2.4. (0) | 2021.01.03 |
| [PRML] 2.4~2.5 (0) | 2020.10.25 |
| [PRML] 2.1~2.2.1 Probability Distributions (0) | 2020.07.26 |




