| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- #링글후기
- 소통챌린지
- 강동구장어맛집
- 링글커리어
- #직장인영어
- 오피스밋업
- 스몰토크
- 영어로전세계와소통하기
- 영어회화
- 링글경험담
- #링글
- 총각네장어
- #체험수업
- 링글리뷰
- #nlp
- 영어공부
- 영어시험
- #영어공부
- 둔촌역장어
- 해외취업컨퍼런스
- 화상영어
- CommunicateWiththeWorld
- Ringle
- #Ringle
- 뉴노멀챌린지
- 링글
- #영어발음교정
- 영어공부법
- 장어랑고기같이
- 성내동장어
- Today
- Total
Soohyun’s Machine-learning
[PRML] 8.4 Inference in Graphical Models 본문
graphical model의 inference 문제를 보자.
그래프에서 관측된 값들로 다른 노드들의 posterior distribution을 구하려고 한다.
앞으로 보게될테지만, graphical structure를 사용해서 추론에 효과적인 알고리즘을 찾을 수도, 이 알고리즘을 알려주는 structure를 만들 수도 있다.
많은 알고리즘들이 그래프상에서의 local messages의 propagate, 전파로 표현할 수 있다.
Bayes Theorem의 graphical interpretation을 생각해보자.
joint distribution $p(x,y)$는 아래와 같이 decompose 할 수 있다.

위의 공식에서 marginal distribution $p(x)$는 latent variable $x$에 대한 prior로 볼 수 있으며,
우리의 목표는 sum rule과 product rule을 써서 이 $x$에 대응하는 posterior distribution을 얻는 것이다.
이는 아래 수식과 같이 나타낼 수 있고,

Bayes Theorem을 써서 계산할 수 있다.
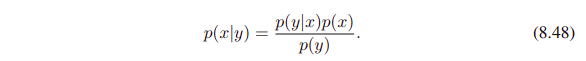
그렇기에 joint distribution $p(x,y)$는 $p(y)$와 $p(x|y)$로 표현할 수 있다.
이제 아래 그림을 보자. 아래에 그래프들은 모두 $p(x,y)$의 표현 형태라고 볼 수 있다.
- (a)는 $p(x,y) = p(x)p(y|x)$의 형태이며,
- (b)는 $y$의 값이 observe된 상태 (shaded node)인 걸 볼 수 있고,
- (c)에서는 $p(y)$와 $p(x|y)$로 나타내는 것이다. ($y$가 observe된 상태이므로, given이다)


위의 그래프가 graphical model의 inference 문제의 가장 심플한 예시이다.
directed graph는 동일한 undirected graph로 바꿀 수 있다.
directed graph는 아래 그림에서 보듯이 하나의 parent node가 있기 때문이고,
directed / undirected 와는 상관없이 완전히 동일한 a set of conditional independence statements로 표현되기 때문이다.

위의 (b) 그래프의 joint distribution은 아래와 같다.

여기서 ψ (psi)로 표현된 것은 potential function을 말한다.
이 점을 감안하고 보면 그냥 (노드간 joint dist를 모두 곱한것에 norm coef.를 곱한 것) 임을 알 수 있다.
이제 각 노드가 $K$개의 states를 갖고 있는, $N$개 노드 (discrete variables)를 생각해보자.
위의 potential function은 K x K의 table로 이루어져 있으며,
따라서 이들의 joint distribution은 $(N-1)K^2$ 의 parameters를 갖고 있다.
($N-1$은 노드들의 숫자이며, $K^2$는 테이블)
chain을 따라서 부분적으로, 어떤 노드 $x_n$에 대한 marginal distribution $p(x_n)$을 찾는, inference problem을 생각해보자. 이때 관측된 노드도 없다고 본다.
정의에 따라, marginal은 $x_n$을 제외한 모든 variables의 joint distribution을 sum하는 것이다. 아래의 수식을 보면 $x_n$은 없는 걸 볼 수 있다.

먼저 joint distribution을 evaluate하고, 그 다음 summation하는 것으로 naive하게 implement 할 수 있다.
$x$에 대해 가능한 값, 각 값에 대한 하나의 숫자들의 set으로 joint distribution을 나타낼 수 있다.
왜냐하면 각각 $K$개의 states를 가진 $N$개의 variables가 있고,
$x$에 대해 $K^N$개의 값들이 있으니
joint distribution의 evaluation & storage라고 볼 수 있고,
$p(x_n)$을 얻기 위한 marginalization 이기도 하다.
---> 이 때문에... chain의 길이 $N$에 따라.. exponentially 하게 크기가 커진다.
Graphical model의 conditional independence properties를 사용해서, 더 효율적인 알고리즘을 얻을 수 있다.
아래 (8.49)의 수식을
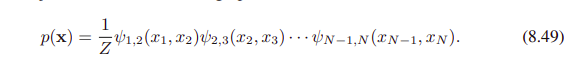
(8.50)과 같이 대체하면..

multiplication과 summations의 순서를 재배열해서, marginal을 더 효과적으로 evaluate 할 수 있다.
$x_N$에 대한 summation을 생각해보면, $x_N$에 dependent한 potential은 하나 뿐이다.

이 수식을 $x_(N-1)$에 대한 summation을 수행하는데에 쓸 수 있다. -> $x_N$을 계산하는, 첫 함수로 준다
또한 이 수식은 아래처럼, 또 다른 potential function과"만" 함께 쓰인다. 이 수식 역시도 $x_(N-1)$이 나타나는 또 다른 위치일 뿐이기 때문이다.

비슷하게 $x_1$에 대한 summation은 오직 potential $\psi_1,_2(x_1, x_2)$와만 관련이 있다. 그래서 $x_2$의 함수를 위해 분리할 수 있고, 이런식으로 쭈욱 간다.
summation이 각각 있으므로, 이게 distribution으로부터 variable을 효과적으로 제거한다.
이는 graph에서 node를 제거하는 것으로 볼 수도 있다.
이 방식으로 potential과 summation을 그룹핑하면, 구하려던 marginal은 아래와 같은 모습으로 표현된다.
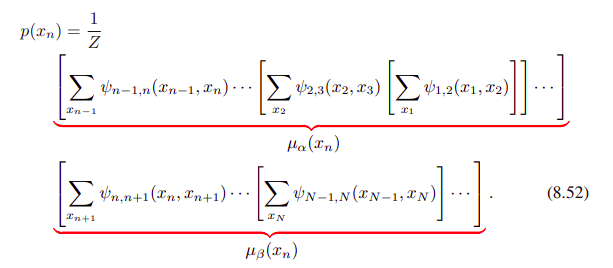
이제 key concept, 분배법칙을 사용해보자.

좌측은 곱셈 두 번에 덧셈 한 번, 총 세 번의 연산을 하지만, 우측은 곱셈 한 번 덧셈 한 번으로 총 두 번의 연산만 하는 것을 볼 수 있다.
이런식으로 marginal을 계산하는데에 드는 cost를 줄여보도록 하자.
두 개의 variables 관련 함수에는, $K$개의 states가 있는데, 각 state에 대해 $N-1$번의 summation을 한다.
$x_1$에 대해 summation을 하는 건, K by K 테이블인 function $\psi_1,_2(x_1,x_2)$와만 관련이 있으며, $O(K^2)$의 cost를 갖는다.
$K$개의 숫자를 가진 resulting vector는 뒤의 function $\psi_2,_3(x_2,x_3)$의 matrix와 곱해지고, 다시 $O(K^2)$의 cost를 가진다.
이는 chain 길이에 linear하게 증가하는데, 이전의 naive한 approach가 chain 길이에 exponential하게 증가했음을 떠올려보면 더 효율적이게 되었음을 알 수 있다.
<br.
여기서 만약에, graph가 fully connected 라면, conditional dependence properties가 없기 때문에, 바로 full joint distribution으로 하면 된다.
graph의 local message를 passing하는 측면에서
marginal $p(x_n)$을 normalization constant $Z$와 두 factors $\mu_\alpha$, $\mu_\beta$의 곱으로 decompose 할 수 있다.
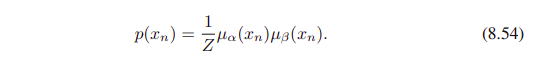
- $1/Z$는 normalization term이며,
- $\mu_\alpha$가 노드 $x_(n-1)$에서 시작해서 노드 $x_n$으로, messages를 forward로 보내며
- $\mu_\beta$는 노드 $x_(n+1)$에서 시작해서 노드 $x_n$으로 messages를 backward로 보내는 녀석이다.
각각의 message는 $K$개 값들의 set으로 이루어져 있고,
이 두 개의 메시지를 곱하는 건, 또 다른 $K$ 값들의 set을 위한, point-wise multiplication으로 볼 수 있다.
여기서 message $\mu_\alpha$ 항목은 재귀적으로 evaluate할 수 있는데, 그 수식은 아래와 같다.

이런식으로 desired node에 도달할 때까지, 재귀적으로 계산해 나간다.
이 수식에서, 두 variables와 관련있는 local potential에 의해,
outgoing message $\mu_\alpha(x_n)$은
incoming message $\mu_\alpha(x_(n-1))$을 곱하는 것으로 얻어진다.
그 다음, node variables에 대해 summing over 한다.
여기까지가 $\mu_\alpha$에 관한 것이었고,
$\mu_\beta$에 관해서 이야기를 할 것이다. 그 과정은 앞의 과정과 비슷하다.
message $\mu_\beta(x_n)$은 노드 $x_n$에서 시작해서 재귀적으로 evaluate 된다.

noramlization constant $Z$는 $x_n$의 모든 states를 sum하는 것으로 쉽게 eval할 수 있다. $O(K)$ 만큼의 computation이 든다.
이제 chain의 모든 노드 $n ∈ {1, ... , N}$에 대해서,
margianls $p(x_n)$을 evaluate 해보자.
위의 프로시저를 각 노드에 대해서 '그냥' 적용해보면, computational cost는 $O(N^2K^2)$이다.
cost가 너무 크기 때문에, 대신에 노드 $x_N$에서 시작하는 message $\mu_\beta(x_(N-1))$을 launch하고,
노드 $x_1$로 돌아가는, corresponding message를 전파해보자.
그리고 비슷하게 $x_1$에서 시작한 message $\mu_\alpha(x_2)$를 launch하고, 대응되는 message를 노드 $x_N$을 향해 가게끔 한다.
만약 graph의 몇몇 노드가 관측되었다면, 거기에 대응되는 variables는 단순히 그들의 관측된 값으로 고정되며, summation은 없다.
이를 보기 위해서.. variable $x_n$을 observed value $\hat{x_n}$로 고정해보자.
그러면 그 효과는 추가 함수 $I(x_n, \hat{x_n})$에 의한 joint distribution으로 곱하는 것으로 나타낼 수 있다.
(여기서 함수 $I$는 $x_n$과 $\hat{x_n}$이 같을 때, 1이 되고, 그렇지 않을때에는 0이 된다.)
이런 함수는 $x_n$을 가진 각 potentials에 흡수될 수 있는데, 함수 자체의 성질 덕분에 $x_n$에 대한 summations만 수행해도 $x_n$과 $\hat{x_n}$이 같은 애들 (1인 애들)만 포함되기 때문이다.
이제 chain에서 이웃하는 두 노드들을 위한 joint distribution $p(x_(n-1), x_n)$을 계산해보자.
single node에 대한 marginal을 구할때와 비슷하지만, 두 variables가 not summed out 된다는 점이 다르다.
이 joint distribution의 수식은 아래와 같다.
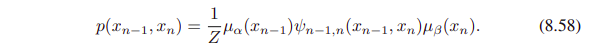
그러니 각 potentials의 all of the sets of variables에 대한 joint distribution을 직접적으로 한 번에 구할 수 있다. (message passing은 complete해야한다. marginal을 얻으려면)
clique potentials를 위해 parametric forms를 쓰길 바라는 것이나,
directed graph로부터 시작할 때의 conditional distribution는 같다.
모든 variables가 관측된 게 아닐때, 이런 potentials의 parameters를 학습하기 위해서, EM 알고리즘을 쓸 수 있다.
그리고 cliques의 local joint distribution (관측된 데이터에 conditioned on 하는)은 E step에서 필요하다.
| 8.4.2 Trees |
노드들의 chain으로 구성된 graph의 inference를 봤다.
더 일반적으로 inference는
tree라고 불리우는 graph의 더 넓은 class를 통해,
local message passing을 써서 효과적으로 수행할 수 있다.
이걸 sum-product 알고리즘으로 generalize 해서 줄거다.

(a) undirected tree
(b) directed graph (하나의 root이 있는 걸 볼 수 있다.)
(c) directed polytree
만약 directed tree를 undirected tree로 바꿀 때, parent가 하나면 moralization step은 link를 추가하지 않았다.
때문에 결과적으로 결과 moralized graph는 undirected tree이다.
directed tree로 나타낸 distribution은 undirected tree로 쉽게 바꿀 수 있고, 그 반대도 마찬가지이다.
만약 directed graph에 있는 노드들이 두 개의 parent 이상으로 갖고 있는데, 여전히 두 노드 사이엔 one path만 있을 경우, 이를 polytree라고 부른다. 위의 그림에서 (c)이다.
| 8.4.3 Factor graphs |
이 다음 섹션에서 보게 될 sum-product algorithm은 undirected / directed trees / polytrees에 해당이 된다.
이제 Factor graph를 보자.
directed / undirected graphs, 두 그래프 모두 a global function of several variables가
그 several variables의 subsets에 대한 factors의 product로 표현할 수 있다.
factor graph는 이 decomposition을,
variables를 나타내는 노드들에 추가로,
factors에 대한 추가 노드들을 도입하는 것으로, explict하게 해낸다.
(variables 노드 따로, factors 노드 따로)
factors의 product form에 있는, a set of variabes에 대한 joint distribution 수식을 보자.

$x_s$ : a subset of variables
각 variable은 $x_i$로 표현하고,
각 factor $f_s$는. 위의 variable에 대응되는 set of variables $x_s$의 함수이다.
위의 (8.59) 수식은 directed graphs의 factorization 정의 (factors $f_s(x_s)$가 local conditional distribution일 때)이며,
아래의 (8.50) 수식이 이 (8.59) 수식의 special case이다.

아래처럼 주어지는 undirected graph는 speical case로, maximal cliques에 대한 potential functions이다.
(여기서 normalization coefficient $1/Z$는 variables의 공집합에 대해 정의된 factor로 볼 수 있다.)
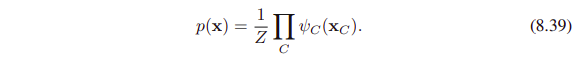
factor graph도 보자.

이 factor graph에서 variables node는 위에 위치하며, 중간이 빈 둥근 모양이고
(additional node인) factor node는 하단에 위치하며, 중간이 찬 사각형 모양이다.
그리고, factor에 depend on하는 variables node와 연결해주는 links들이 있다.
이 factor graph는 아래의 수식에 대한 것으로, factorization 측면에서 표현된 distribution이다.

여기서 두 factors $f_a(x_1, x_2)$와 $f_b(x_1, x_2)$는 same set of variables (즉, $x_1$, $x_2$)로 정의되는 걸 볼 수 있다.
undirected graph에서 이런 two factors의 product는 단순하게 same clique potential로 뭉칠 수 있다.

(a) a single clique potential $\psi(x_1, x_2, x_3)$에 대한 undirected graph
(b) factor $f(x_1, x_2, x_3) = \psi(x_1, x_2, x_3)$의 factor graph, (a)와 같은 distribution이다.
(c) (b)와 또 다른 형태의 factor graph. factors는 $f_a(x_1, x_2, x_3)f_b(x_1, x_2) = \psi(x_1, x_2, x_3)$를 만족한다.
다 같은 distribution이지만, 다른 형태로 나타냈다.
factor graph는 bipartite 하다고 할 수 있다.
두 개의 분리된 종류의 노드 (variable node / factor node)로 이루어져 있고,
모든 links는 반대되는 종류의 노드 사이에 있기 때문이다.
그래서 일반적으로 factor graph는 항상 two rows of nodes로 그려진다. (위에 그림에서도 보이듯이)
undirected graph 측면에서 표현된 distribution이 있다면, factor graph로 쉽게 변환할 수 있다.
이를 위해, original undirected graph의 노드들에 대응하는 variables node를 만들고,
maximal cliques $x_s$에 대응하는 추가적인 factor nodes를 만든다.
(factors $f_s(x_s)$는 clique potentials과 동일한 set이다.)
여기서 체크할 것은 같은 undirected graph에 대응하는 몇 개의 다른 factor graph가 있을 수 있다는 것이며,
directed graph를 factor graph로 바꾸는 과정도 undirected graph와 비슷하고, 이 역시도 multiple factor graphs가 있을 수 있다.
directed graph의 노드들에 대응하는 variables nodes를 만들고
conditional distribution에 대응되는 factor nodes를 만든다.
그리고 적합한 links를 추가하면 된다.
하단 그림의 factorization은 $p(x_1)p(x_2)p(x_3 | x_1, x_2)$이며,
(b)는 $f(x_1, x_2, x_3) = p(x_1)p(x_2)p(x_3 | x_1, x_2)$를 나타내고
(c)는 $f_a(x_1) = p(x_1), f_b(x_2) = p(x_2)$와 $f_c(x_1, x_2, x_3) = p(x_3 | x_1, x_2)$를 나타낸다.

이 conversion은 시작도 결과물도 tree였는데,
tree라는 건 loop가 없으며, 두 노드간에는 1개의 path만이 있다는 걸 뜻한다.
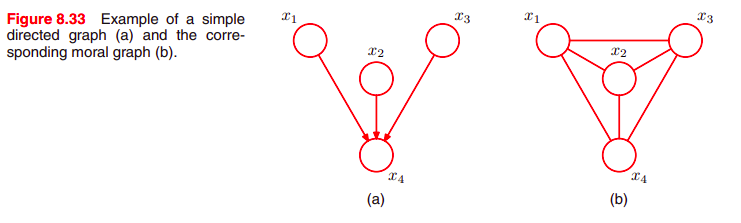
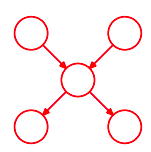
directed polytree같은 경우, undirected graph로 바꿀 때, moralization step (marrying parents!) 때문에 loops가 생겨버리는데...
그럼에도 그 결과물은 역시 tree이다.

(a) a directed polytree이고
(b)는 polytree를 undirected graph로 바꾼 결과물이다. loops가 보인다.
(c) polytree를 factor graph로 바꾼 결과이다. tree structure를 유지하고 있음을 볼 수 있다.
사실 node의 연결된 parents 때문에 생긴 directed graph의 local cycles은, 위의 그림에서도 보이다시피
factor graph로 바뀔 때 사라진다. 하단 figure (8.44)에서 보이다시피, 적합한 factor function이 정의되기 때문이다.

directed / undirected graph에 대해 서로 다른 multiple factor graphs가 있을 수 있음을 봤다.
이게 factor graphs를, factorization의 정확한 형태를 더 알기쉽게 해준다.

위의 세 그래프는 모두 같은 것을 말하고 있다.
(b)는 general form $p(x) = f(x_1, x_2, x_3)$의 joint distribution
(c)는 (b)보다 더 세부적인 factorization, $p(x) = f_a(x_1, x_2)f_b(x_1, x_3)f_c(x_2, x_3)$를 보이며,
어떠한 conditional independence properties에도 해당하지 않는다.
'Machine Learning > PRML' 카테고리의 다른 글
| [PRML] 8. Graphical Models (0) | 2021.06.06 |
|---|---|
| [PRML] 6.4.1~6.4.4 Kernel Methods (0) | 2021.04.04 |
| [PRML] 4.1.6 ~ 4.2.4. (0) | 2021.01.03 |
| [PRML] 2.4~2.5 (0) | 2020.10.25 |
| [PRML] 2.1~2.2.1 Probability Distributions (0) | 2020.07.26 |




